728x90
오늘은 분류 문제 3번째!
오늘은 머신러닝 지도학습에서 가장 직관적이고 설명하기 쉬운 분류 모델인
결정 트리(Decision Tree) 분류에 대해 공부해보겠습니다!
결정 트리란?
결정 트리는 말 그대로 "질문을 따라가며 결정을 내리는 나무(tree) 형태"의 모델입니다.
각 분기점(노드)에서는 하나의 **조건(특징값 기준)**을 검사하고,
그 결과에 따라 왼쪽/오른쪽으로 가지(branch)를 타며
**최종 리프 노드에서 분류 결과(클래스)**가 결정됩니다!
예시로 설명하면?
[특징: 나이 ≤ 30?] → YES → [소득 ≤ 5000?] → YES → 클래스 A
→ NO → 클래스 B
→ NO → [직업 = 학생?] → YES → 클래스 A
→ NO → 클래스 C
이처럼 질문을 계속 따라가다 보면 마지막 노드에서 결과가 나옵니다.
결정 트리의 장점
- 직관적이고 설명 가능성(Explainability)이 높음
- 전처리나 정규화가 필요 없음
- 시각화가 쉬움 → 비즈니스 설명에 적합
단점.....
- 데이터에 민감하고 과적합(overfitting)이 잘 발생할 수 있음
- 작은 데이터에선 잘 동작하지만, 복잡해질수록 랜덤포레스트나 부스팅을 함께 사용해야 안정적임!
분기를 나누는 기준!
트리는 데이터를 나누는 기준으로 아래 두 가지 대표적인 불순도(impurity) 척도를 사용합니다.
- 지니 불순도(Gini Impurity)
- 대부분의 라이브러리에서 기본값
- 특정 클래스로 분류될 확률의 제곱합을 사용
- 엔트로피(Entropy)
- 정보 이론 기반 척도
- 예측의 불확실성을 수치로 표현
Gini = 1 - Σ (p_i)^2
Entropy = -Σ (p_i * log2(p_i))
그럼 이제 실습! 결정 트리 분류 코드
import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import make_classification
from sklearn.tree import DecisionTreeClassifier, plot_tree
# 1. 데이터 생성
X, y = make_classification(n_samples=100, n_features=2,
n_informative=2, n_redundant=0,
n_clusters_per_class=1,
random_state=42)
# 2. 결정 트리 모델 생성
model = DecisionTreeClassifier(max_depth=3, criterion='gini')
model.fit(X, y)
# 3. 분류 경계 시각화
x_min, x_max = X[:, 0].min()-1, X[:, 0].max()+1
y_min, y_max = X[:, 1].min()-1, X[:, 1].max()+1
xx, yy = np.meshgrid(np.linspace(x_min, x_max, 300),
np.linspace(y_min, y_max, 300))
Z = model.predict(np.c_[xx.ravel(), yy.ravel()]).reshape(xx.shape)
plt.contourf(xx, yy, Z, alpha=0.3, cmap="Pastel1")
plt.scatter(X[:, 0], X[:, 1], c=y, edgecolors='k', cmap="Pastel1")
plt.title("결정 트리 분류 경계 (depth=3)")
plt.show()- make_classification: 2D 분류 데이터 생성
- DecisionTreeClassifier: 결정 트리 분류기
- max_depth: 트리 깊이를 제한하여 과적합 방지
- criterion: 분기 기준 (gini 또는 entropy)
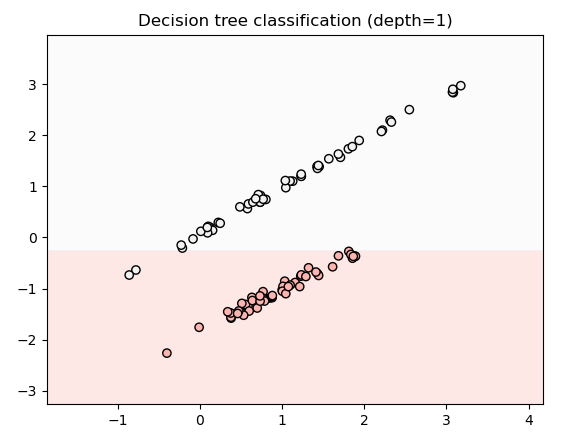
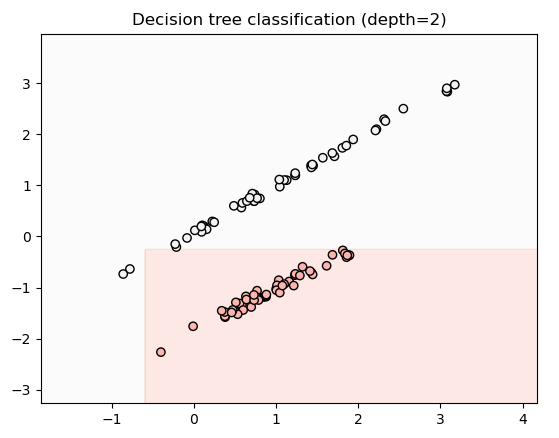
결정 트리는 데이터를 직사각형(축 기준 분할) 형태로 나눕니다.
깊이가 제한될수록 좀 더 정확하게 분류되는걸 볼 수 있었습니다!

트리 구조 시각화!
plt.figure(figsize=(10,6))
plot_tree(model, filled=True, feature_names=["X0", "X1"])
plt.title("결정 트리 구조 시각화")
plt.show()

어.... 위와 같은 방식으로 분류가 된거 같은디.... 이건 잘 모르겠네요...
추가로 결정트리에서의 비선형 분포에서는 어떻게 나올지 실습해 보았습니다.
비선형 분포에선?
from sklearn.datasets import make_moons
# 1. 비선형 데이터 생성
X, y = make_moons(n_samples=200, noise=0.25, random_state=42)
# 2. 트리 모델 학습
model = DecisionTreeClassifier(max_depth=4)
model.fit(X, y)
# 3. 시각화
xx, yy = np.meshgrid(np.linspace(X[:, 0].min()-1, X[:, 0].max()+1, 300),
np.linspace(X[:, 1].min()-1, X[:, 1].max()+1, 300))
Z = model.predict(np.c_[xx.ravel(), yy.ravel()]).reshape(xx.shape)
plt.contourf(xx, yy, Z, alpha=0.4, cmap="Set3")
plt.scatter(X[:, 0], X[:, 1], c=y, cmap="Set3", edgecolors='k')
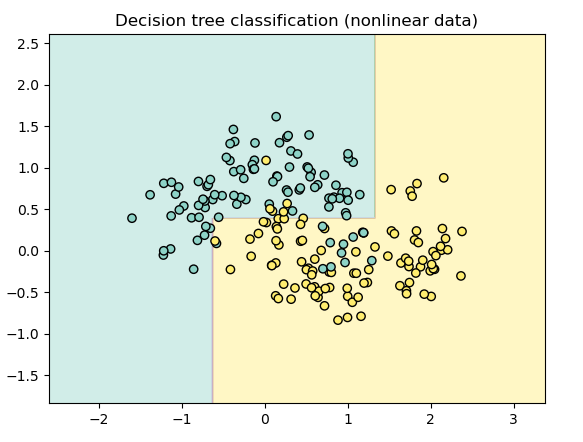
plt.title("결정 트리 분류 (비선형 데이터)")
plt.show()
비선형 구조도 어느 정도는 따라가지만, 경계가 "계단형"으로... 부드럽게 표현이 안되는.....
이런 부분에서 랜덤포레스트나 부스팅과 결합하여 결과를 개선한다고 합니다!
오늘은 여기서 끝! 정리하고 다음글로 돌아오겠습니다!
결정트리 정리
- 결정 트리는 질문 기반의 분기 구조로 분류 문제를 해결함
- 해석이 쉬워서 실무 적용도 많음
- 과적합 방지를 위해 max_depth, min_samples_leaf 등의 제약이 필요
- 분할 기준: Gini, Entropy
- 비선형 문제도 어느 정도 다룰 수 있지만, 더 복잡한 문제는 앙상블 기법이 필요함
다음글은 랜덤포레스트!
틀린점이 있다면 댓 달아주세요!

728x90
'공부공부 > 얕게 둘러본 부분들' 카테고리의 다른 글
| [인공지능/AI _ 4] - 머신러닝 > 지도 학습 > 분류 (서포트 벡터 머신 실습) (0) | 2025.05.04 |
|---|---|
| [인공지능/AI _ 3] - 머신러닝 > 지도 학습 > 분류 (로지스틱 회귀 이진분류/다중 분류 실습) (1) | 2025.05.03 |
| [인공지능/AI _ 2] - 머신러닝 > 지도 학습 > 회귀 (선형 회귀와 다항 회귀 실습) (1) | 2025.03.20 |
| [인공지능/AI _ 1] - 머신 러닝의 정의 및 학습 방법 정리 (0) | 2025.03.18 |
| ChatGpt api 테스트 해보기! (Postman 사용) (0) | 2023.05.03 |




댓글