오늘은 분류 문제 2번째!
오늘은 머신러닝의 지도학습 중,
분류 문제를 해결하는 또 하나의 강력한 방법인 서포트 벡터 머신(SVM) 에 대해 공부해보겠습니다!
분류란 다시 정리!
앞 글에서도 다뤘지만, 간단히 요약하면
- 분류(Classification)는 데이터를 미리 정해진 클래스(Label)로 나누는 작업!
- 출력값이 범주형(클래스)인 문제에 사용됩니다.
SVM (Support Vector Machine)이란?
서포트 벡터 머신은 두 클래스 사이의 경계(결정 경계)를 정의하고,
그 경계를 기준으로 데이터를 분류하는 모델입니다.
주된 목적은?
"클래스 사이의 마진(Margin)을 최대화하는 최적의 경계(초평면)를 찾는 것!"
SVM의 핵심 개념들
1. 결정 경계 (Decision Boundary)
- 데이터를 분류하는 선 혹은 초평면 (2D에선 선, 3D 이상에선 평면)
2. 마진 (Margin)
- 결정 경계와 각 클래스에서 가장 가까운 데이터(서포트 벡터) 사이의 거리
3. 서포트 벡터 (Support Vector)
- 결정 경계에 가장 가까이 있는 데이터 포인트들
- 이 점들만이 결정 경계를 직접적으로 정의함!
시각적으로 이해해보면?
- 단순히 잘 나누는 선을 그리는 게 아니라,
- 가장 여유롭게(=마진이 최대화되도록) 두 클래스를 나누는 선을 찾습니다.
선형 SVM 수식 (이진 분류)
SVM은 아래와 같은 형식의 결정 경계를 학습합니다:
w · x + b = 0- w: 결정 경계의 방향 벡터 (가중치)
- x: 입력 데이터
- b: 편향 (bias)
이 선에서의 거리, 그리고 마진을 기반으로 최적화 문제를 풀어 w, b를 구합니다.
비선형 데이터는? → 커널 트릭 (Kernel Trick)
현실 데이터는 선형적으로 구분되지 않는 경우가 많습니다.
이를 해결하기 위해 SVM은 커널 함수를 사용해 입력 데이터를 고차원 공간으로 매핑합니다.
예: 2차원 공간의 원형 분포 데이터를 3차원으로 올려서 평면으로 나눌 수 있게 만드는 느낌!
대표적인 커널 종류
- Linear (기본 선형 커널)
- Polynomial (다항 커널)
- RBF (Radial Basis Function, 가우시안 커널 – 가장 많이 사용됨)
- Sigmoid (신경망 커널)
실습! SVM 분류 코드
import numpy as np
import matplotlib.pyplot as plt
from sklearn import datasets
from sklearn.svm import SVC
# 1. 데이터 생성
X, y = datasets.make_classification(n_samples=100, n_features=2,
n_informative=2, n_redundant=0,
n_clusters_per_class=1,
random_state=42)
# 2. 모델 생성 (선형 SVM)
model = SVC(kernel='linear')
model.fit(X, y)
# 3. 시각화용 그리드 생성
x_min, x_max = X[:, 0].min()-1, X[:, 0].max()+1
y_min, y_max = X[:, 1].min()-1, X[:, 1].max()+1
xx, yy = np.meshgrid(np.linspace(x_min, x_max, 500),
np.linspace(y_min, y_max, 500))
grid = np.c_[xx.ravel(), yy.ravel()]
Z = model.predict(grid).reshape(xx.shape)
# 4. 시각화
plt.contourf(xx, yy, Z, alpha=0.3, cmap='coolwarm')
plt.scatter(X[:, 0], X[:, 1], c=y, cmap='coolwarm', edgecolors='k')
plt.title("SVM Classification")
plt.show()
우선 저번 로지스틱스 회귀와 동일하게 make_classification를 이용해서 데이터를 생성해주고,
SVM모델을 생성해주는데, kernel='linear'를 통해 선형 분류 모델을 선언해 줍시다!
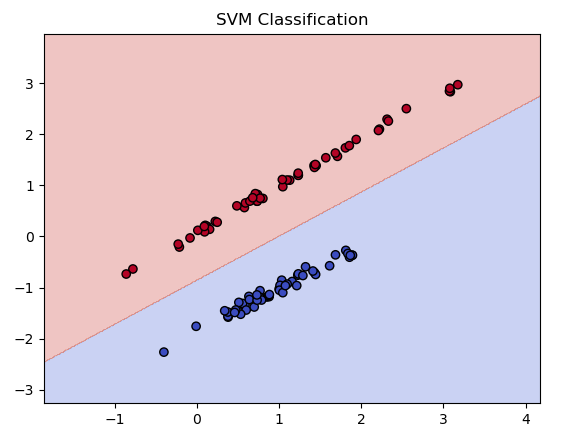
결과는.... 오... 굳굳 잘 나눠지는것 같습니다.
선형 분류는..... 좀 쉬워보이니까...
이번엔 비선형 데이터에 대한 SVM
import numpy as np
import matplotlib.pyplot as plt
from sklearn import datasets
from sklearn.svm import SVC
# 1. 비선형 분포 데이터 생성
X, y = datasets.make_circles(n_samples=200, factor=0.5, noise=0.1, random_state=0)
# 2. RBF 커널 SVM 모델
model = SVC(kernel='rbf', gamma='scale')
model.fit(X, y)
# 3. 예측 시각화
xx, yy = np.meshgrid(np.linspace(X[:, 0].min()-1, X[:, 0].max()+1, 500),
np.linspace(X[:, 1].min()-1, X[:, 1].max()+1, 500))
Z = model.predict(np.c_[xx.ravel(), yy.ravel()]).reshape(xx.shape)
plt.contourf(xx, yy, Z, alpha=0.3, cmap='PuBu')
plt.scatter(X[:, 0], X[:, 1], c=y, cmap='PuBu', edgecolors='k')
plt.title("SVM - nonlinear ")
plt.show()
다른건 다 동일한데, 데이터셋을 비선형으로 잘 나뉘도록 만들어주고,
이번엔 kernel='rbf'로 가우시안 커널을 선택해서 분류를 진행해줍시다.
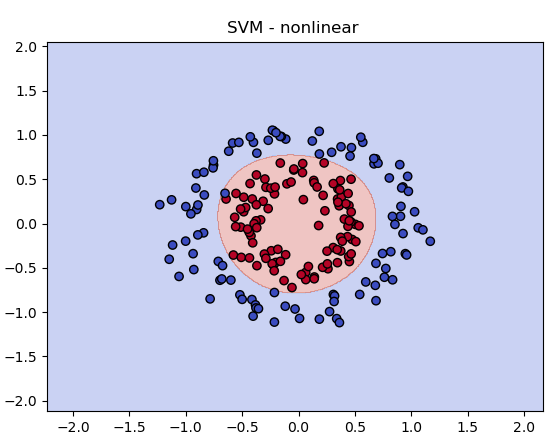
비선형도 위와 같이 잘 나뉘는걸 볼 수 있었습니다.
이번글도 여기서 마무리!
SVM 정리
- SVM은 마진을 최대화하는 분류기
- 서포트 벡터만으로 경계를 정의함
- 선형 분류와 비선형 분류 모두 가능
- 비선형 문제는 커널 트릭으로 해결 (특히 RBF 커널!)
다음글은 결정트리와 랜덤포레스트!로 돌아오겠습니다!
틀린점이 있다면 댓 달아주세요!

'공부공부 > 얕게 둘러본 부분들' 카테고리의 다른 글
| [인공지능/AI _ 5] - 머신러닝 > 지도 학습 > 분류 (결정 트리 분류 실습) (0) | 2025.05.05 |
|---|---|
| [인공지능/AI _ 3] - 머신러닝 > 지도 학습 > 분류 (로지스틱 회귀 이진분류/다중 분류 실습) (1) | 2025.05.03 |
| [인공지능/AI _ 2] - 머신러닝 > 지도 학습 > 회귀 (선형 회귀와 다항 회귀 실습) (1) | 2025.03.20 |
| [인공지능/AI _ 1] - 머신 러닝의 정의 및 학습 방법 정리 (0) | 2025.03.18 |
| ChatGpt api 테스트 해보기! (Postman 사용) (0) | 2023.05.03 |




댓글