오늘은 분류 문제!
오늘은 지도학습 중 하나인 분류! 문제에 대해 이야기해보겠습니다!
분류란?
분류는 말 그대로 어떤 데이터를 미리 정해진 클래스로 나누는 작업입니다.
- 예를 들어 사진을 보고 고양이인지 개인지 판별한다면? → 분류
- 환자의 기록을 보고 질병 유무를 판별한다면? → 분류
- 이메일이 스팸인지 아닌지를 판단한다면? → 분류
즉, 분류는 출력값이 연속적인 숫자가 아니라, 정해진 레이블(Label) 중 하나로 나오는 문제입니다.
분류의 종류
- 이진 분류
→ 정답이 두 가지 (예: 스팸/정상, Yes/No, 0/1) - 다중 분류
→ 정답이 세 가지 이상 (예: 숫자 인식 0~9)
대표적인 분류 알고리즘
- 로지스틱 회귀 (Logistic Regression)
- 서포트 벡터 머신 (SVM)
- 결정 트리 (Decision Tree)
- 랜덤 포레스트 (Random Forest)
- 인공 신경망 (Neural Networks) 등
그중에서도 오늘은 분류의 가장 기본적이고 핵심적인 모델!
바로 "로지스틱 회귀(Logistic Regression)" 를 다뤄보겠습니다!
로지스틱 회귀 (Logistic Regression)
로지스틱 회귀는 이름에 회귀(regression)가 들어가 있지만, 사실 분류(classification) 문제를 해결하는 데 사용됩니다!
즉, 연속적인 값을 예측하는 선형 회귀와는 달리, 결과값을 두 개의 클래스 중 하나로 분류하는 모델입니다.
예시
예를 들어 이메일 스팸 여부(스팸/정상), 환자의 질병 유무(Yes/No)처럼
결과가 "0 또는 1", "True 또는 False"로 구분되는 문제에 활용됩니다.
음... 사용되는 수식 부분!
선형 회귀처럼 로지스틱 회귀도 입력값 x와 가중치 w, 편향 b를 사용합니다.
하지만 출력값이 확률(0~1) 이어야 하므로, 직선이 아닌 S자형 곡선(Sigmoid 함수) 를 사용해 출력값을 조정합니다.
- 시그모이드 함수
σ(z) = 1 / (1 + exp(-z))- 여기서 z = wx + b
- z가 커질수록 출력은 1에 가까워지고,
- 작아질수록 0에 가까워집니다!
- 분류 기준
로지스틱 회귀는 예측 결과가 확률로 나오기 때문에, 보통 0.5를 기준으로 분류합니다:
- σ(z) ≥ 0.5 → 클래스 1
- σ(z) < 0.5 → 클래스 0
(기준값은 상황에 따라 다르게 설정할 수도 있음)
- 비용함수: 교차 엔트로피 (Cross-Entropy)
선형 회귀에서 MSE를 썼다면,
로지스틱 회귀에서는 분류 문제에 적합한 이진 교차 엔트로피를 사용합니다.
Cost = -[ y*log(p) + (1-y)*log(1-p) ]- y: 실제 정답 (0 or 1)
- p: 모델의 예측값 (확률)
- 경사하강법 (Gradient Descent)
비용을 최소화하기 위해 경사하강법으로 w, b 값을 업데이트합니다.
이는 선형 회귀와 유사하지만, 시그모이드 함수의 미분을 사용해 업데이트하는 점이 다릅니다.
실습! 로지스틱 회귀 코드
import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import LogisticRegression
# 1. 데이터 생성
np.random.seed(0)
x = np.random.randn(100, 2)
y = (x[:, 0] + x[:, 1] > 0).astype(int) # 단순한 선형 분류 기준
# 2. 모델 학습
model = LogisticRegression()
model.fit(x, y)
# 3. 예측 및 시각화
xx, yy = np.meshgrid(np.linspace(-3, 3, 100), np.linspace(-3, 3, 100))
grid = np.c_[xx.ravel(), yy.ravel()]
probs = model.predict_proba(grid)[:, 1].reshape(xx.shape)
plt.contourf(xx, yy, probs, levels=[0, 0.5, 1], cmap="RdBu", alpha=0.6)
plt.scatter(x[:, 0], x[:, 1], c=y, cmap="OrRd", edgecolors='k')
plt.title("Logistic Regression")
plt.show()
해당 코드도 sklearn에서 제공해주는 로지스틱스 회귀함수를 이용하면! 바로 실습이 가능합니다.
로지스틱스 회귀는 단순 이진 분류가 기본적인 구조이기에 따로 설정할 값은 없습니다!
위 코드의 결과는 특정경계를 기점으로 분류된 것을 볼수 있습니다!

그런데!
로지스틱 회귀는 무조건 이진 분류?
앞서 예제에서는 로지스틱 회귀를 사용해 0 또는 1로 나누는 이진 분류 문제를 해결했지만,
로지스틱 회귀는 다중 클래스 분류에도 활용될 수 있습니다!
1. One-vs-Rest (OvR, 일대다 방식)
클래스가 여러 개인 경우, 각 클래스를 **"해당 클래스 vs 나머지 전부"**로 나눠서
여러 개의 이진 분류기를 학습시키는 방식입니다.
예를 들어, 분류할 클래스가 3개라면:
- A vs (B + C)
- B vs (A + C)
- C vs (A + B)
각각의 모델에서 확률이 가장 높은 클래스를 최종 결과로 선택합니다.
2. 소프트맥스 회귀 (Softmax Regression)
이 방법은 다중 로지스틱 회귀(Multinomial Logistic Regression) 이라고도 불리며,
시그모이드 함수 대신 Softmax 함수를 사용하여 모든 클래스의 확률 분포를 예측합니다.
- 예: 클래스가 3개면 출력이 [0.2, 0.3, 0.5] 이런 식의 확률 벡터
- 총합은 항상 1이 되며, 가장 큰 값을 갖는 클래스가 예측 결과가 됩니다.
로지스틱스 다중 분류! 코드
import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import make_classification
from sklearn.linear_model import LogisticRegression
# 1. 다중 클래스 데이터 생성
X, y = make_classification(n_samples=300, n_features=2,
n_informative=2, n_redundant=0,
n_classes=3, n_clusters_per_class=1,
random_state=42)
# 2. 로지스틱 회귀 (multinomial + softmax)
model = LogisticRegression(multi_class='multinomial', solver='lbfgs')
model.fit(X, y)
# 3. 시각화용 meshgrid
x_min, x_max = X[:, 0].min()-1, X[:, 0].max()+1
y_min, y_max = X[:, 1].min()-1, X[:, 1].max()+1
xx, yy = np.meshgrid(np.linspace(x_min, x_max, 300),
np.linspace(y_min, y_max, 300))
grid = np.c_[xx.ravel(), yy.ravel()]
Z = model.predict(grid).reshape(xx.shape)
# 4. 결과 시각화
plt.contourf(xx, yy, Z, alpha=0.3, cmap="Accent")
plt.scatter(X[:, 0], X[:, 1], c=y, edgecolors='k', cmap="Accent")
plt.title("다중 클래스 로지스틱 회귀")
plt.show()
우선 다중 클래스를 생성하고, 로지스틱스함수에 설정값을 부여해주어야합니당
다중 클래스 설정값들!
make_classification(
X: 입력값 (300개의 샘플, 2차원 좌표)
y: 클래스 레이블 (0, 1, 2의 세 가지 클래스)
n_informative=2: 두 개의 특성이 분류에 실제로 사용됨
n_classes=3: 세 개의 클래스
random_state: 매번 같은 데이터가 생성되도록 고정
)
model = LogisticRegression(multi_class='multinomial', solver='lbfgs')
그 다음 로지스틱스 회귀를 다중 분류방식으로 하겠다! (>> Softmax 회귀 방식 사용 )
그리고 최적화 방법으로 L-BFGS 알고리즘 사용하겠다! (Softmax와 잘 어울림)
multi_class='ovr'로 바꾸면 One-vs-Rest 방식으로 변경된다고 합니다...
결과는 아래처럼! ( multinomial이나... ovr이나 비슷하네요...ㅎ )
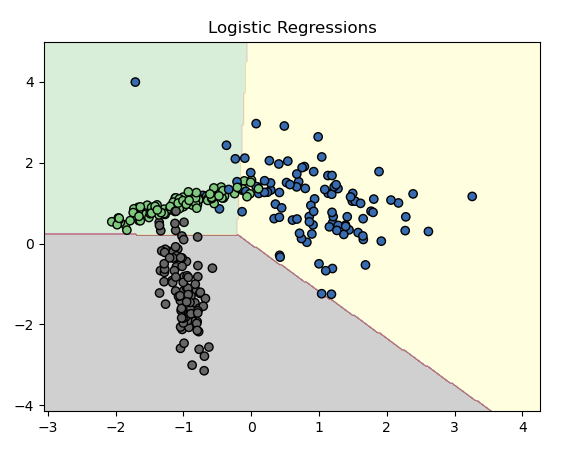

아래와 같은 차이가 있다고 합니다! (데이터에 따라 다를수도?)
| 항목 | multi_class='ovr' (One-vs-Rest 방식) | multi_class='multinomial' (Softmax 방식) |
| 분류 방식 | 각 클래스를 하나씩 "나머지와 비교" | 전체 클래스 확률을 동시에 예측 |
| 예측 구조 | 클래스 수만큼 이진 분류기 생성 | 하나의 모델에서 모든 클래스 처리 |
| 수학적 기반 | 시그모이드 함수 (이진) | 소프트맥스 함수 (다중) |
| 장점 | 구현이 단순, 이진 문제에 유리 | 다중 클래스 간 상호작용 반영 가능 |
| 단점 | 클래스 간 정보 공유 없음 | 수치적으로 조금 더 복잡 |
오늘은 여기서 끝! 정리하고 마치겠습니다!
로지스틱 회귀 정리
- 선형 회귀는 수치 예측, 로지스틱 회귀는 이진 분류
- wx + b를 시그모이드로 변환하여 확률 출력
- 확률이 기준 이상이면 클래스 1, 미만이면 클래스 0
- 비용함수는 이진 교차 엔트로피, 최적화는 경사하강법
- 로지스틱 회귀는 기본적으로 이진 분류 모델
- 하지만 OvR, Softmax 기법으로 다중 분류 문제에도 확장 가능
다음 글에서는 여러 개의 클래스를 분류할 수 있는 서포트 벡터 머신(SVM)에 대해서 마저 알아보도록 하겠습니다!
틀린점이 있다면 댓 달아주세요!

'공부공부 > 얕게 둘러본 부분들' 카테고리의 다른 글
| [인공지능/AI _ 5] - 머신러닝 > 지도 학습 > 분류 (결정 트리 분류 실습) (0) | 2025.05.05 |
|---|---|
| [인공지능/AI _ 4] - 머신러닝 > 지도 학습 > 분류 (서포트 벡터 머신 실습) (0) | 2025.05.04 |
| [인공지능/AI _ 2] - 머신러닝 > 지도 학습 > 회귀 (선형 회귀와 다항 회귀 실습) (1) | 2025.03.20 |
| [인공지능/AI _ 1] - 머신 러닝의 정의 및 학습 방법 정리 (0) | 2025.03.18 |
| ChatGpt api 테스트 해보기! (Postman 사용) (0) | 2023.05.03 |




댓글