카라츠 바 알고리즘이란?
수 백 자리 이상의 큰 수의 곱셈할 때 사용하는 알고리즘으로
곱셈의 올림수 연산을 생략한 상태로 계산 후 덧셈, 뻴셈연산으로 더욱 빠르게 계산할 수 있게 해주는 알고리즘!
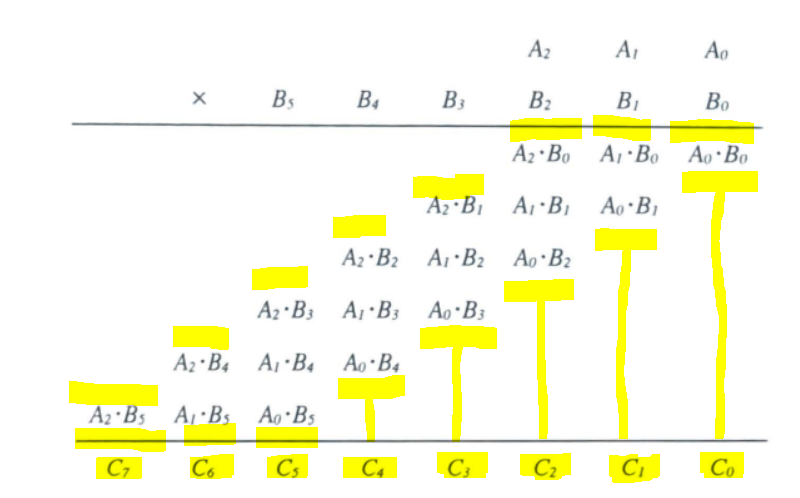
형식은 아래처럼 한자리 곱셈으로 곱을 해주고 나머지는 모두 덧셈으로 풀리게 됩니다!

예시를 보면 이렇게!

위에서 보이는 것처럼 한자리 곱셈을 제외한 모든 것들이 덧셈으로 해결 가능합니다!
이제 코드로 한 번해보시죠!
void nomalize(vector<int>& num) {//마지막 자릿수 계산
num.push_back(0);
for (int i=0; i<num.size(); i++) {
if (num[i] < 0) {
int borrow = (abs(num[i])) + 9 / 10;
num[i+1] -= borrow;
num[i] += borrow * 10;
} else {
num[i+1] += num[i]/10;
num[i] %= 10;
}
}
while(num.size() > 1 && num.back() == 0) num.pop_back();
}
vector<int> kara(const vector<int>& a, const vector<int>& b) {//int형 수 2개를 계산하는 카라츠바 알고리즘!
vector<int> c(a.size() + b.size() + 1, 0);//최대숫자 사이즈 a+b+1
for (int i=0; i<a.size(); i++) {
for (int j=0; j<b.size(); j++) {
c[i+j] += a[i] *j[j];//벡터에 자릿수 계산 안 한 채로 추가!
}
}
normalize(c); //자릿수 마지막계산
return c; // 답 출력!
}
생각보다 간단한 알고리즘이지만 참 다양하게 사용될 수 있었습니다.
[C++] 알고스팟/분할정복 - 팬미팅
문제 링크 https://algospot.com/judge/problem/read/FANMEETING algospot.com :: FANMEETING 팬미팅 문제 정보 문제 가장 멤버가 많은 아이돌 그룹으로 기네스 북에 올라 있는 혼성 팝 그룹 하이퍼시니어가 데뷔..
dontdiethere.tistory.com
이 문제를 보시면 단순 곱셈을 하기 위한 알고리즘이 아닌 약간 조합 문제도 해결 가능해 보이는 알고리즘이었습니다.
1줄의 사람들과 반대편의 사람들이 모두가 악수를 하는지 세어보는 문제인데 (악수는 0 포옹은 1)
이런 식으로 곱셈을 이용하면 조합으로 사용할 수 있었습니다.
그러고 나서 자릿수를 상관하지 않는 카라츠 바 알고리즘을 이용하여 c의 값을 구할 수 있고 몇 명이 악수를 했는지도 구할 수 있었습니다!
결론은! 조합에서도 곱셈을 사용할 수 있고, 무언갈 카운트하려고 할 때 위의 방법처럼 풀 수 있다는 점이 중요한 것 같습니다!
다른 블로그!
카라츠바의 빠른 곱셈 (Karatsuba algorithm)
카라츠바의 빠른 곱셈 카라츠바의 빠른 곱셈 알고리즘은 수백, 수만자리나 되는 큰 두개의 정수를 곱하는 알고리즘이다. 필요성 카라츠바 알고리즘을 소개하기에 앞서, 두자릿수 이상의 두 수
invincibletyphoon.tistory.com
틀린 점이 있다면 댓 달아주세요!

'공부공부 > 알고리즘!' 카테고리의 다른 글
| 유니온 파인드 [Union Find] 알고리즘 (0) | 2023.06.03 |
|---|---|
| 정렬 알고리즘[2] -- 버블 정렬 알고리즘 (0) | 2022.06.28 |
| 정렬 알고리즘[1] -- 선택 정렬 알고리즘 (0) | 2022.06.28 |
| 알고스팟(algospot) 32장 네트워크 유량 (0) | 2022.05.22 |
| 알고스팟(algospot) 31장 최소 스패닝 트리(크루스칼과 프림 알고리즘) (0) | 2022.05.22 |




댓글