32.1 도입
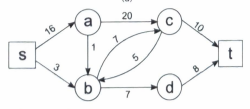
이런 그래프가 하나 있을 때 크기가 10인 데이터는 아마 s--> a--> c--> t라는 경로만 지나가게 될 것입니다.
그런데 여기서
데이터 전송 시 데이터를 쪼개서 여러 경로로 동시에 전송 가능하다면?
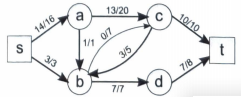
나눠서 더 빠르게! 전송 가능--> 이것이 네트워크 유량!
좀 더
유량 네트워크
- 간선의 용량이라는 속성이 존재하는 방향 그래프
- 항상 세 가지 속성을 만족해야 한다.
- 용량 제한 속성 - 각 간선의 유량(이동할 데이터량)은 해당 간선의 용량(이동할 수 있는 총량) 초과 x
- 유량의 대칭성 - u에서 v라 흘러올 경우 udptjsms 음수의 유량을 보내는 것이라 생각하자-->?
- 유량의 보존 - 나가고 들어오는 유량은 항상 같아야 함!
32.2 포드 -폴 커슨 알고리즘
(이보다 빠른 알고리즘도 많지만! 알고리즘 문제를 푸는 데는 문제가 없음)
원리--> 모든 간선의 유량을 0으로 두고 시작해서 시작 정점에서 도착 정점까지의 경로를 찾아 유량 보내기를 반복
--> 경로는..?--> 잔여용량이 남은 간선들만을 사용하는 너비 우선 탐색을 이용해 경로탐색!
(깊이 탐색을 안 쓰는 이유?)--> 수행 시간이 총유량에 비례하기 때문에 너비 탐색이 더 유리
더 이상 경로를 탐색할 수 없을 때 종료!
#include <iostream>
#include <cstring>
#include <vector>
#include <queue>
using namespace std;
const int INF=(1<<30);
const int MAX_V = 100;
int V;
//capacity[u][v]=u에서 v로 보낼 수 있는 용량
//flow[u][v]=u에서 v로 흘러가는 유량 (반대 방향인 경우 음수)
int capacity[MAX_V][MAX_V], flow[MAX_V][MAX_V];
//flow[][]를 계산하고 총 유량을 반환한다.
int networkflow(int source, int sink){
//flow를 0으로 초기화 한다.
memset(flow, 0, sizeof(flow));
int totalFlow=0;
while(true){
//너비 우선 탐색으로 증가 경로를 찾는다.
vector<int> parent(MAX_V, -1);
queue<int>q;
parent[source]=source;
q.push(source);
while(!q.empty() && parent[sink]==-1){
int here=q.front();
q.pop();
for(int there=0; there<V; ++there)
if(capacity[here][there] - flow[here][there] > 0 &&
parent[there]==-1){
q.push(there);
parent[there]=here;
}
}
//증가 경로가 없으면 종료한다.
if(parent[sink]==-1) break;
//증가 경로를 통해 유량을 얼마나 보낼지 결정한다.
int amount = INF;
for(int p=sink; p!=source; p=parent[p])
amount=min(capacity[parent[p]][p] - flow[parent[p]][p], amount);
//증가 경로를 통해 유량을 보낸다.
for(int p=sink; p!=source; p=parent[p]){
flow[parent[p]][p]+=amount;
flow[p][parent[p]]-=amount;
}
totalFlow+=amount;
}
return totalFlow;
}
-최소 컷 최대 유량 정리
경로상 간선에 유량을 최대로 해서 보내야 하는데 아무 간선이나 선택해도 될까..?
---> 이러한 경우가 없다는 것을 증명하는 정리!
한 네트워크 유량의 컷에서는 2가지의 속성이 항상 성립!
1. 컷의 유량은 소스에서 싱크로 가는 총유량과 같다.
2. 컷의 유량은 용량과 같거나 더 작다
이러한 속성을 가지고 최소 컷을 구하면-->
1. 소스에서 잔여용량이 있는 간선을 통해
갈 수 있는
갈 수 없는 정점의 집합을 나눔!
2. 두 집합의 용량, 유량을 비교
*컷? 출발지(소스)와 도착지(싱크)가 각각 다른 집합에 속하도록 두 개의 집합으로 나눈 것!
---> 좀 더 읽어보기
C++ - 포드 풀커슨 방법(에드몬드 카프 알고리즘) 과 최소 컷 최대유량
출처 : 알고리즘 문제 해결 전략 포드 풀커슨 알고리즘은 최초로 고안된 네트워크 유량 알고리즘으로 그 개...
blog.naver.com
유량 그래프 ① : 포드-풀커슨 알고리즘
유량 그래프의 정의와, 최대유량 문제를 해결하는 포드-풀커슨 알고리즘, 그리고 그 정당성을 알아봅시다.
velog.io
인접 리스트로도 구현 가능
--> 유량의 상쇄를 통한 역방향 간선으로도 유량을 보낼 필요가 있기에 (u, v)가 추가된다면 유령 간선 (v, u)도 추가해야 함!
32.3 네트워크 모델링
예제)
마일리지로 여행하기 --> 어떤 자원을 효율적으로 분배하는 그런 문제
도난당한 조각상 --> 최소 컷을 사용하는 문제
32.8 이분 매칭
두 개의 정점 그룹이 존재할 때
모든 간선(경로)의 용량이 1이면서 양쪽 정점이 서로 다른 그룹에 속하는 그래프를 이분 그래프
이러한 이분 그래프에서 두 그룹을 이어주는 것이 이분 매칭입니다.
네트워크 유량으로 간단하게 풀기 가능
but 포드 폴 커슨 알고리즘을 이용해서 풀기에는 복잡;;
좀 더 간단한 알고리즘 구현
// Algorithm Analysis
// 이분 매칭 알고리즘 (Bipartite Matching)
#include <iostream>
#include <vector>
#define MAX 101
using namespace std;
vector<int> vtx[MAX]; // 정점 vtx
int slt[MAX]; // vtx가 점유하고 있는 정점
bool done[MAX]; // 처리 여부
int n = 5; // 정점 수, 간선 수
bool dfs(int x) {
// 연결된 모든 정점에 대해 들어갈 수 있는 지 시도
for (int i = 0; i < vtx[x].size(); i++) {
int p = vtx[x][i];
// 이미 처리한 정점은 고려하지 않음
if (done[p]) continue;
done[p] = true;
// 비어있거나 점유 정점에 더 들어갈 공간이 있는 경우
if (slt[p] == 0 || dfs(slt[p])) {
slt[p] = x;
return true;
}
}
return false;
}
int main() {
vtx[1].push_back(1);
vtx[1].push_back(3);
vtx[1].push_back(5);
vtx[2].push_back(1);
vtx[2].push_back(2);
vtx[3].push_back(5);
vtx[4].push_back(3);
vtx[5].push_back(2);
int cnt = 0; // 매칭 수
for (int i = 1; i <= n; i++) {
fill(done, done + MAX, false);
if (dfs(i)) cnt++;
}
printf("%매칭 %d번 성공\n", cnt);
for (int i = 1; i < MAX; i++) {
if (slt[i] != 0) {
printf("%d => %d\n", slt[i], i);
}
}
}최대 유량이 정해져 있어서 깊이 우선 탐색을 사용!
경로가 저장됨
예제)
여행사진 문제 --> 사진과 유적지를 매칭
도미노로 직사각형 채우기 --> 칸과 칸이 변을 맞대고 있을 때 두정점을 간선으로 연결
--> 격자 그래프!--> 체스판
이를 통해 이분 매칭 사용 가능
[알고리즘] 이분 매칭 알고리즘 (Bipartite Matching)
이분 매칭 알고리즘 (Bipartite Matching) 두 개의 정점 그룹이 존재할 때 모든 간선(경로)의 용량이 1이면서 양쪽 정점이 서로 다른 그룹에 속하는 그래프를 이분 그래프(Bipartite Graph)라고 말합니다
yjg-lab.tistory.com
32.13 더 공부할거리
한번 읽어보기!
'공부공부 > 알고리즘!' 카테고리의 다른 글
| 정렬 알고리즘[2] -- 버블 정렬 알고리즘 (0) | 2022.06.28 |
|---|---|
| 정렬 알고리즘[1] -- 선택 정렬 알고리즘 (0) | 2022.06.28 |
| 알고스팟(algospot) 31장 최소 스패닝 트리(크루스칼과 프림 알고리즘) (0) | 2022.05.22 |
| 알고스팟(algospot) 21 장 트리의 구현과 순회 (0) | 2022.05.15 |
| 알고스팟(algospot) 20장 문자열 (0) | 2022.05.15 |


댓글