선형회귀란?
몇개의 주어진 값들로 하나의 직선을 만들어 표현하는 방법
ex) 공부시간과 성적의 연관 그래프
이 그래프를 그리기 위해 최소제곱법이라는 공식을 사용
각각의 평균의 값과 모든 실제값들의 차의 합을 이용해 기울기를 구하는방법으로 기울기a는
구할수 있고 y절편 b 는
*→>>>>mean(x)=x의 평균 mean(y)=y의 평균
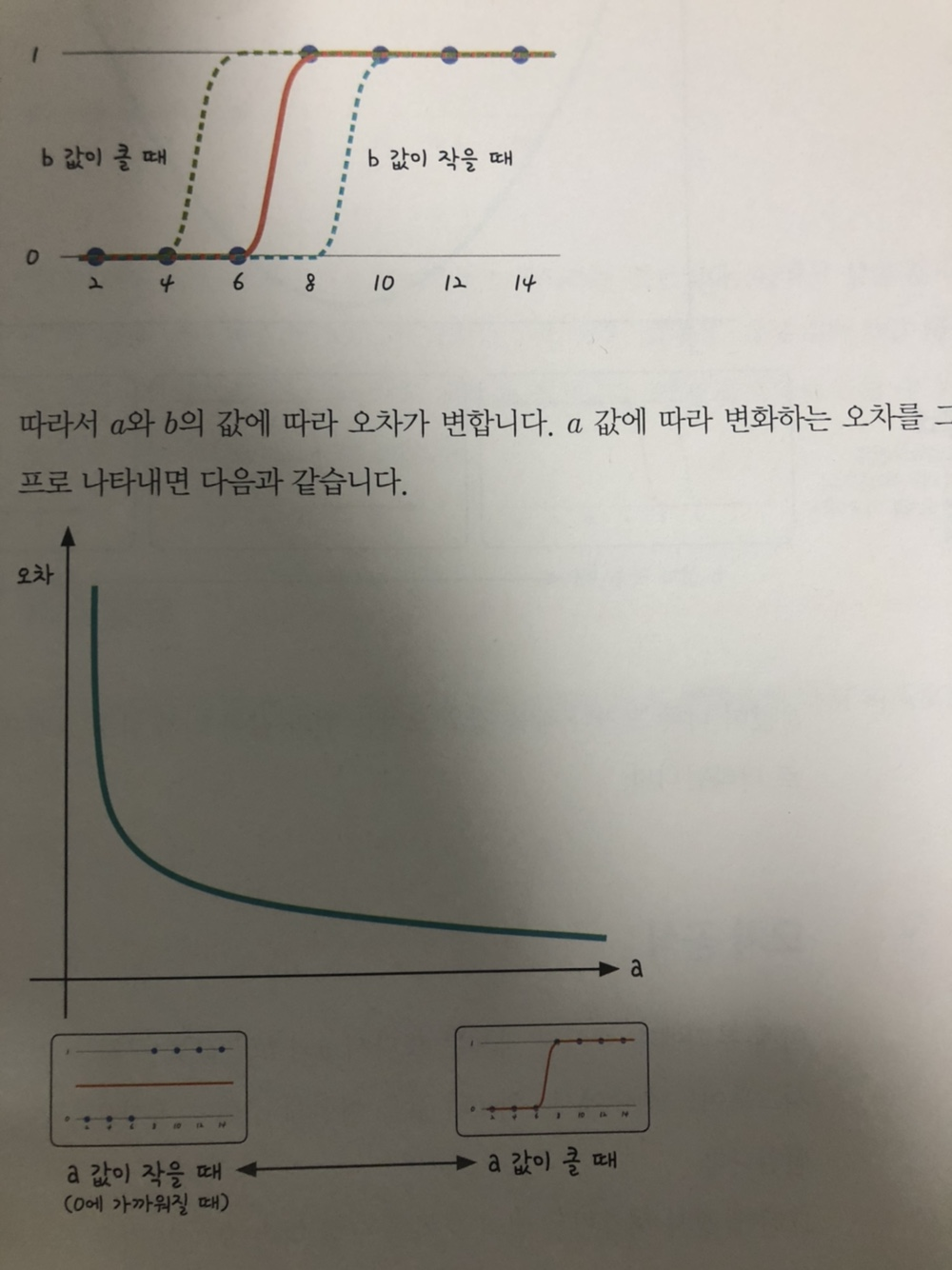
그런데 여기서 x,y값 뿐만아니라 z,x,v,c,e,g등등 더 많은 값들이 사용될때 최소제곱법으로 풀기에는 무리가 있음!
그래서 사용하는게 평균제곱근 오차!
실제값-예측값 들을 제곱하여 모두 합한값의 평균을 구하고 거기다 근을 씌워주면 평균제곱근 오차가 나오게된다
여기서 나오는 값은 지금까지 만든 그래프와 실제 값들이 얼마나 차이나는지 오차를 구해주는 것이다.
이것을 왜 구하는가?? 이것을 어떻게 사용하는가는 다음 경사 하강법에서 알수있음!
경사하강법!
위에서 구한 오차값과 기울기 a값 사이의 그래프를 그려보면
이렇게 그릴수 있고, 경사하강법에서는 오차가 최소가 될수 있는점m을 찾기 위한 방법이다.
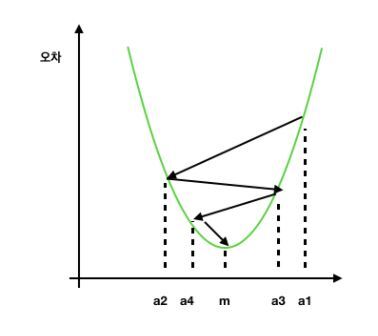
보시다시피 2차함수 그래프에서 최솟점은 접선의 기울기가 0일때이다. 이걸 이용해서 구해야한다.
지금 기울기가 a1이라고 하자 기울기가 m이될때 까지 어떻게 이동해야할까
여기서 사용하는것이 학습률! 최적의 학습률 을 찾아 그만큼 이동시켜 점점 접선의 기울기를 낮춰가는것이다!
*학습률이 너무크면 m으로안가고 점점 오차가 커진다..... 적절한 학습률 필요!
일단 학습률이 정해지면 각각의 값들은
그 값들을 기준으로 편미분한 다음
학습률을 곱해 원래값에서 빼준다.
—> 기울기에 대한 경사하강법
- 평균 제곱 오차 식에서 y에 원래식 대입
- a에 대해 편미분 —>> -가 왜붙지..? 78페이지
- a=a-a에대해 편비분한값*학습률
- 반복횟수만큼 계속해서 반복—학습
다중선형회귀도 다를게 없음! 위의 방법 똑같이!
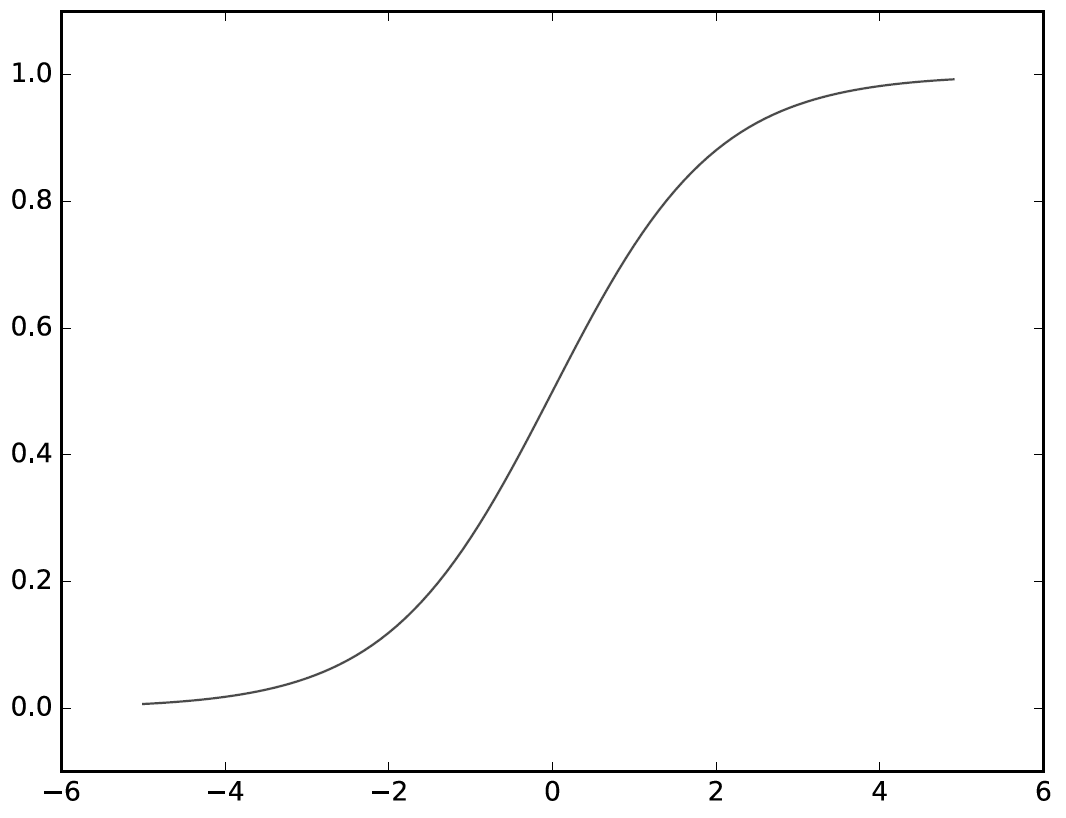
로지스틱스 회귀?
참과 거짓만을 구별하는 방법
— 시그모이드 함수 이용
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
data=[[2,0],[4,0],[6,0],[8,1],[10,1],[12,1],[14,1]]
x_data=[i[0] for i in data]
y_data=[i[1] for i in data]
a=0
b=0
lr=0.05
def sigmoid(x):
return 1/(1+np.e**(-x))
for i in range(2001)://경사하강법
for j in range(len(data)):
a_diff=x_data[j]*(sigmoid(a*x_data[j]+b)-y_data[j])
b_diff=sigmoid(a*x_data[j]+b)-y_data[j]
a=a-a_diff*lr
b=b-b_diff*lr
if i%1000==0:
print("epoch=%.f,기울기=%.04f,절편=%.04f"%(i,a,b))
plt.scatter(x_data,y_data)
plt.xlim(0,15)
plt.ylim(-.1,1.1)
x_range=np.arange(0,15,0.1)
plt.plot(np.arange(0,15,0.1),np.array([sigmoid(a*x+b)for x in x_range]))
plt.show()
이렇게 경사하강법을 이용해서 시그모이드 함수모양을 결정해준다.
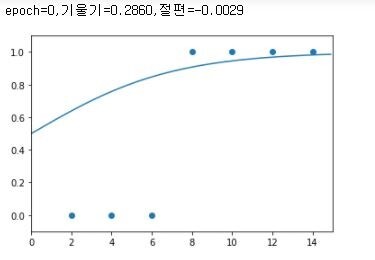
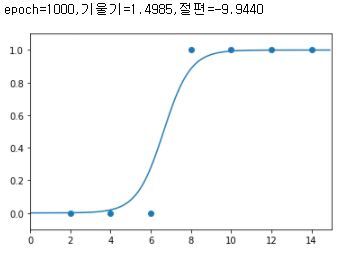
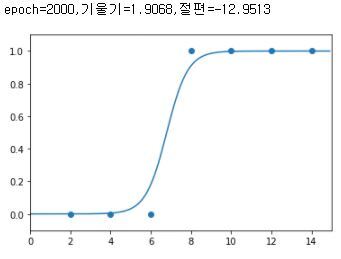
틀린점이 있다면 댓 달아주세요!

'공부공부 > 얕게 둘러본 부분들' 카테고리의 다른 글
| ChatGpt api 테스트 해보기! (Postman 사용) (0) | 2023.05.03 |
|---|---|
| 구글 지도 api 기본 마커 지우기 및 테마 변경 (1) | 2023.04.11 |
| 퍼셉 트론..! (0) | 2022.03.06 |



댓글