15.2 계산기하의 도구
1 ) 벡터의 구현!
struct vector2
{
double x, y;
//생성자를 explicit으로 지정하면 vector2를 넣을 곳에 잘못해
//실수가 들어가는 일을 방지
explicit vector2(double x_ = 0, double y_ = 0) :x(x_), y(y_)
{ }
//두 벡터의 비교
bool operator==(const vector2 &rhs) const
{
return x == rhs.x&&y == rhs.y;
}
bool operator<(const vector2 &rhs) const
{
return x != rhs.x ? x < rhs.x : y < rhs.y;
}
//벡터의 덧셈과 뺄셈
vector2 operator+(const vector2 &rhs) const
{
return vector2(x + rhs.x, y + rhs.y);
}
vector2 operator-(const vector2 &rhs) const
{
return vector2(x - rhs.x, y - rhs.y);
}
//실수로 곱셈
vector2 operator*(double rhs) const
{
return vector2(x*rhs, y*rhs);
}
//벡터의 길이를 반환
double norm() const
{
return hypot(x, y);
}
//방향이 같은 단위 벡터를 반환
//영벡터에 대해 호출한 경우 반환 값은 정의되지 않는다
vector2 normalize() const
{
return vector2(x / norm(), y / norm());
}
//x축의 양의 방향으로부터 이 벡터까지 반시계 방향으로 잰 각도
double polar() const
{
return fmod(atan2(y, x) + 2 * PI, 2 * PI);
}
//내적/외적의 구현
double dot(const vector2 &rhs) const
{
return x * rhs.x + y * rhs.y;
}
double cross(const vector2 &rhs) const
{
return x * rhs.y - rhs.x*y;
}
//이 벡터를 rhs에 사영한 결과
vector2 project(const vector2 &rhs) const
{
vector2 r = rhs.normalize();
return r * r.dot(*this);
}
};
극각도 계산하는 polar()함수 중요
atan2()함수 사용--> #include <cmath> 라이브러리
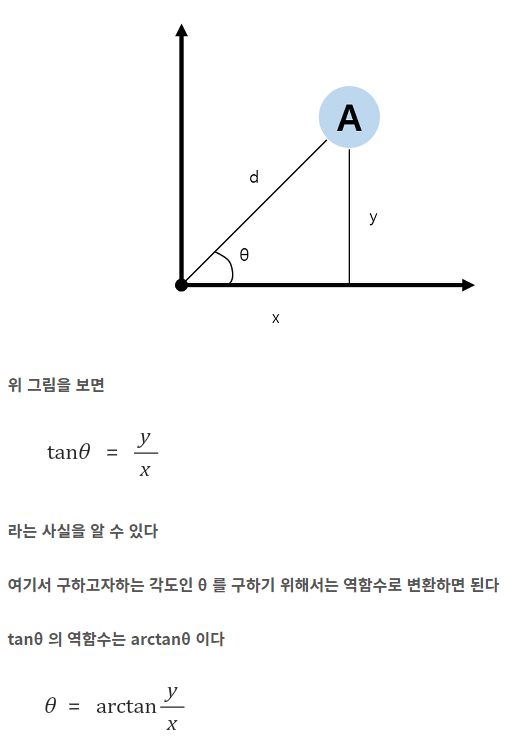
[C/C++] atan2 함수로 각도 구하기 (극 좌표계)
직각 좌표계? 극 좌표계? 평면 상에서 어떤 점의 위치 또는 원점에 대한 상대적 위치를 나타내야 한다고 할 때 우리는 좌표계를 이용한다 그 좌표계를 표현하는 방법은 대표적으로 2가지가 있다
choryeonworkshop.tistory.com
어렵...
2 ) 점과 직선,선분의 표현 - 점을 방정식이나 좌표로 나타내면 변수 많아짐 --> 벡터로 나타내면 간결하게 풀기 가능!
double howmuchCloser(vector2 p, vector2 a, vector2 b)
{
return (b - p) • norm() - (a - p) .norm1() ;
}
3) 벡터의 내적과 외적!
내적 --> 두 벡터의 사이각을 구할때, 벡터의 사영을 구할때 사용(당연? : 내적이 0이면 서로 직각이다)
외적 -->두 벡터에 수직인 벡터를 구할때, 면적 계산 할 때(절대값!), 두 벡터의 방향을 판별할때 사용

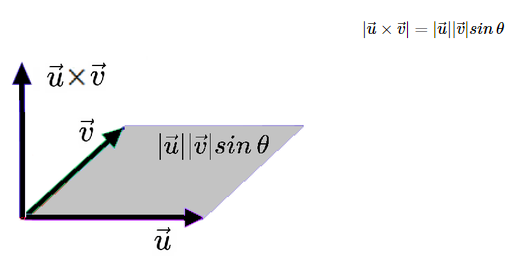
042. 내적 vs 외적
# 내적 | 內積 | inner product **적**은 '쌓는다'는 뜻의 한자이고, 여기서는 '곱한다'는 뜻이다. 벡터의 곱하기는 두 가지 정의가 있는데, 내적은 벡터를 ...
wikidocs.net
15.3 교차와 거리,면적
1 ) 직선과 직선의 교차
벡터를 이용해 방정식으로 만들어서 풀자...
boot linelntersection(vector2 a, vector2 b, vector2 c, vector2 d, vect or2& x) {
//.cross--> 외적
double det = (b - a).cross(d - c);
//두 선이 평행
if(fabs(det) < EPSIL) return false;
x = a + (b-a) * ((c-a).cross(d-c) / det) ;
return true;
}
2 ) 선분과 선분의 교차
두선분간의 관계
1. 두 선분이 서로 안겹침
2. 두 선분이 한점에서 만남
3. 두 선분이 겹침
4. 한선분이 다른선분에 포함됨
3 ) 교차하는지만 볼 때 --> 두선분의 사이각? 확인해서 평행인지만 확인
//두 벡터의 방향성을 판단하는 ccw() 함수 구현
//원점에서 벡터 b가 벡터 a의 반시계 방향이면 양수, 시계 방향이면 음수
//평행이면 0을 반환
double ccw(vector2 a, vector2 b)
{
return a.cross(b);
}
//점 p를 기준으로 벡터 b가 벡터 a의 반시계 방향이면 양수, 시계 방향이면 음수
//평행이면 0을 반환
double ccw(vector2 p, vector2 a, vector2 b)
{
return ccw(a - p, b - p);
}
4) 점과 선 사이의 거리--> 내적
//점과 선 사이의 거리를 계산하는 함수 pointToLine()의 구현
//점 p에서 (a, b) 직선에 내린 수선의 발을 구한다
vector2 perpendicularFoot(vector2 p, vector2 a, vector2 b)
{
return a + (p - a).project(b - a);
}
//점 p와 (a, b) 직선 사이의 거리를 구한다
double pointToLine(vector2 p, vector2 a, vector2 b)
{
return (p - perpendicularFoot(p, a, b)).norm();
}
각 문제들
15.4 핀볼 시뮬레이션--> 튕겨난 반사각에 맞는 벡터 계속 만들어가기
15.6 다각형
1 ) 다각형의 종류?
단순다각형
볼록다각형? 단순다각형이랑 약간 다른듯?
오목다각형 찌그러진 다각형?
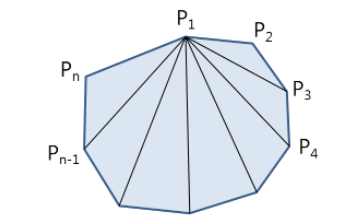
2 ) 면젹 구하기
삼각형의 세점+ 외적이면 그삼각형의 면적 구하기 가능!
다각형을 삼각형으로?
//단순 다각형의 넓이를 구하는 area() 함수
//주어진 단순 다각형 p의 넓이를 구한다
//p는 각 꼭지점의 위치 벡터의 집합으로 주어진다
double area(const vector<vector2> &p)
{
double result = 0;
for (int i = 0; i < p.size(); i++)
{
int j = (i + 1) % p.size();
result += p[i].x*p[j].y - p[j].x*p[i].y;
}
return fabs(result) / 2.0; //오목 다각형 고려하여 절대값
}
3 ) 내부/ 외부 판별
-->점을 기준으로 한쪽으로 쭉 반직선 만들어서 다각형이랑 몇번겹치는지 확인
홀수번이면 내부에 있음!
예외) 선이 겹친다? --> 점을 지난다는뜻 --> 조금만 값을 올린다!
//주어진 점이 단순 다각형 내부에 포함되어 있는지 확인하는 isInside() 함수
//점 q가 다각형 p 안에 포함되어 있을 경우 참, 아닌 경우 거짓 반환
//q가 다각형의 경계 위에 있는 경우의 반환값은 정의되어 있지 않다
bool isInside(vector2 q, const vector<vector2> &p)
{
int crosses = 0;
for (int i = 0; i < p.size(); i++)
{
int j = (i + 1) % p.size();
//(p[i], p[j])가 반직선을 세로로 가로지르는가?
if ((p[i].y > q.y) != (p[j].y > q.y))
{
//가로지르는 x 좌표를 계산
double atX = (p[j].x - p[i].x)*(q.y - p[i].y) / (p[j].y - p[i].y) + p[i].x;
if (q.x < atX) //q보다 오른쪽에 있는가
crosses++;
}
}
//내부에 있는 점이라면 오른쪽으로 반직선을 그릴 경우 다각형과 홀수번 겹침
//외부라면 짝수번 겹침
return crosses % 2 > 0;
}
각 문제들
15.7 보물섬-- 서덜랜드 호지맨
다각형 클리핑
다각형 클리핑 알고리즘(Polygon Clipping Algorithm)은 다각형으로 다른 다각형을 잘라내는 알고리즘입니다. 많이 사용하는 다각형 클리핑 알고리즘으로는 서덜랜드-호지맨 알고리즘(Sutherland-Hodgman Alg
hellogaon.tistory.com
15.9 너드인가 너드가 아닌가--선물포장 알고리즘
15.11 계산기하와 알고리즘 디자인 패턴
1 ) 평면 스위핑
스위핑 : 쓸고지나가며 해결하기!
2 ) 예제 : 직사각형 합집합의 면적
잘라서 일반적인 직사각형으로 만들어 풀기
-- 다각형 교집합도 잘라서 구하기 가능
-- 교차하는 선분의 여부 탐색도 구간을 잘라서 구할수있음
3 ) 회번하는 캘리퍼스
볼록 다각형의 지름
15.12 자주하는 실수와 유의점들
1 ) 퇴화 도형
상식적이지 않은 도형?
-- 일직선에 점이 3개
-- 서로 평행,겹치는 선분들
-- 넓이가 0
등등 존재할수있는지 생각해보기!
2 ) 직교 좌표계와 스크린 좌표계
직교좌표계 스크린 좌표계
0,2 0,0 1,0 2,0 3,0
0,1 0,1
0,0 1,0 2,0 3,0 0,2
이런거? 잘생각하기!
3 ) 다른실수들
되도록이면 정수를 주로 사용하자?
acos asin atan같은 함수는 사용 자제
함수사용시 입력값을 잘 확인하자 --> 약간의 오차발생도 치명적--> 입력제한을 두는것도방법?
ex ) sqrt(max(0.0,x))
9.26 읽어보기!
'공부공부 > 알고리즘!' 카테고리의 다른 글
| 알고스팟(algospot) 20장 문자열 (1) | 2022.05.15 |
|---|---|
| 알고스팟(algospot) 19장 큐와 스택, 데크 (0) | 2022.05.15 |
| 알고스팟 (algospot) 9장 동적계획법 테크닉 (0) | 2022.05.08 |
| 최소신장트리!(프림과 크루스칼) (0) | 2022.03.04 |
| 다익스트라, 플로이드와샬, 벨만포드에 대해서! (0) | 2022.03.04 |



댓글