프로그래머스
코드 중심의 개발자 채용. 스택 기반의 포지션 매칭. 프로그래머스의 개발자 맞춤형 프로필을 등록하고, 나와 기술 궁합이 잘 맞는 기업들을 매칭 받으세요.
programmers.co.kr
문제요약!
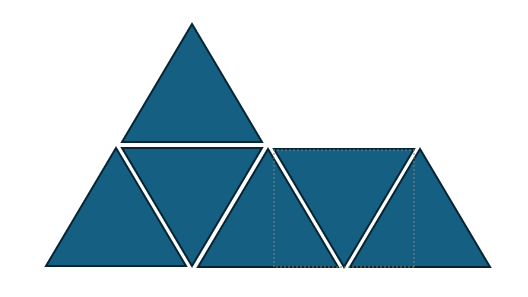
위와 같이 삼각 타일들을 이어붙인 타일에
마름모 타일과 정삼각형 타일을 섞어 붙일 수 있는 경우의 수를 구하는 문제!
주어지는 입력값은 윗변의 삼각형의 유무와 길이! 입력값에 따라 아래처럼 구성됩니다.
ex) [1,0,0] ,n=3
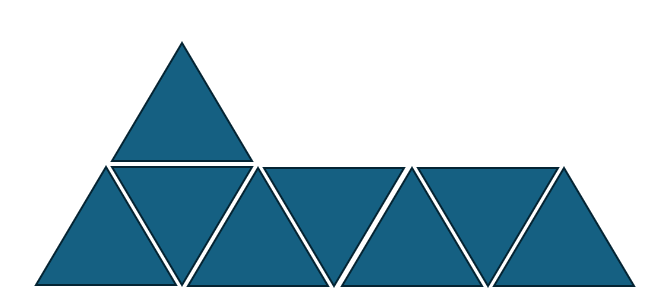
[0,0,0] , n=3
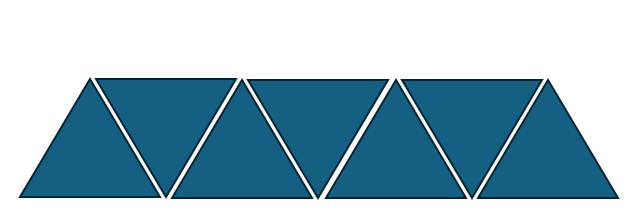
그림부터가 쉽지 않은 문제처럼 보입니다....
가장 처음 드는 생각은 규칙이 존재하지 않을까?
=>> 점화식! DP였습니다.
그래서 일단 규칙을 찾아보기로 하였습니다.
저는 삼각형을 기준으로 생각해 보았습니다.
먼저 이 문제에서 덮고 싶어하는 모양을 구역별로 나누어 생각해보면
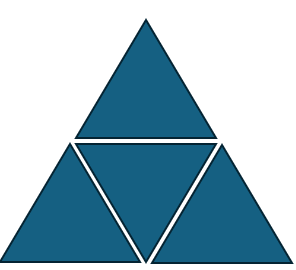
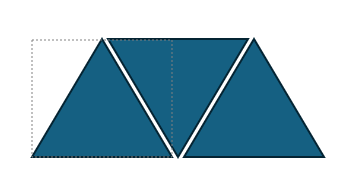
윗 삼각형이 있는 부분과 없는 부분으로 구분지을 수 있습니다.
여기서
삼각형 하나를 마름모와 정삼각형으로 만드는 방법은 총 4가지
1. 모두 정삼각형으로 덮기
2,3,4 번 각각의 모양의 마름모를 섞어 덮기

사다리꼴을 덮는 방법은 총 3가지
1. 모두 정삼각형으로 덮기
2, 3 번 각각의 모양의 마름모를 섞어 덮기
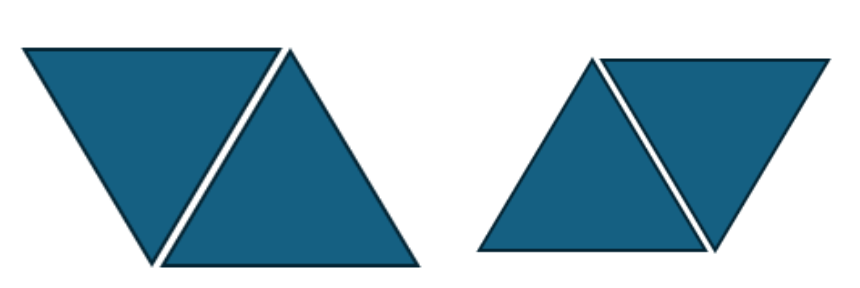
이렇게 가짓수들이 나뉜다는것을 알 수 있었습니다
이제 이렇게 만들어지는 방법의 수만 세어 주면 되는데,
여기서 +
아래와 같은 마름모로 덮는 경우에는 다음 구역에 영향을 줄 수 있다는 점만 생각해주면 될 듯합니다.

(모두 삼각형으로 덮는 방법의 경우는 아래처럼 생각해줍시다!)

그럼 이제 숫자들을 나열해봅시다.
tops = [1,1,0,1] 일때
첫번째 구역 (윗 삼각형 있음) 에서의 가짓수는 4
이중 한가지의 경우만 다음 구역에 영향을 준다는 부분을 생각하며 다음 구역으로 이동합니다.
두번째 구역 (윗 삼각형 있음) 에서의 가짓수도 4이겠지만
이전 구역에서 영향을 받는 경우를 생각해주면
아래처럼 가짓수가 나뉜다는걸 알 수 있습니다.
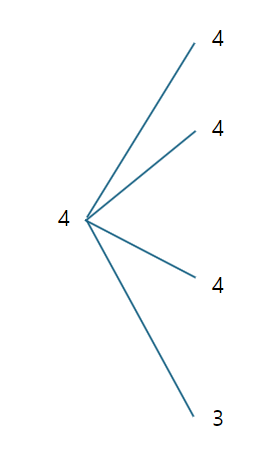
이제 세번째 구역(윗 삼각형 없음)에서는 가짓수가 3
그리고 이전 구역에서 영향을 받는 부분을 생각해주면 아래처럼!
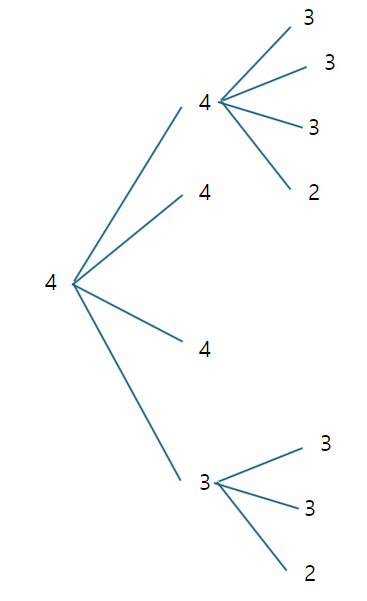
이렇게 계속해서 가짓수를 구성해나갈 수 있었습니다.
그리고 마지막 구역을 구성해주고 끝부분의 경우의 수를 모두 더해주면 = 모든 경우의 수를 구할 수 있습니다!
여기까지 생각해본뒤 먼저 재귀를 통한 함수를 구성해 보았습니다.
규칙에 맞게끔 계속해서 실행되는 재귀함수
//재귀를 통한 풀이?
//
// 경우의 수 풀이 기기
void CountTri(int n,int count,vector<int>& tops) { // 현재 위치 , 전 삼각형에서의 영향이 있는지 , 윗 삼각형배열
int count_Tri = 0; // 각각의 삼각형의 경우의 수 값
if (n == tops.size()) {// 끝 도달
answer = (answer+ count) % 10007;
return;
}
if (tops[n] == 0) { // 윗 삼각형 없음
for (int i = 0; i < count-1; i++) {
CountTri(n + 1, 3, tops);
}
CountTri(n + 1, 2, tops);
}
else { // 윗삼각형 ㅇㅇ
for (int i = 0; i < count - 1; i++) {
CountTri(n + 1, 4, tops);
}
CountTri(n + 1, 3, tops);
}
}
int solution(int n, vector<int> tops) {
if (tops[0] == 0) { // 첫 삼각형 윗변 x
CountTri(1, 3, tops);
}
else {
CountTri(1, 4, tops);
}
return answer;
}
옳은 답을 출력해 주지만.... n의 값이 100000이나 되는데 이걸 재귀로 풀기에는 문제가 있었습니다.
이제 여기서 dp를 통한 재귀함수로 변경하여 구성해주겠습니다.

먼저 점화식을 구성하기 위한 규칙들을 찾아보겠습니다.
여기 까지 구성을 하다보니 규칙을 찾는 부분은 어렵지 않았습니다.
1. 현재구역이 삼각형일때, 이전 구역에서 영향을 받으면 (4-1), 안받으면 4
현재구역이 삼각형이 아닐때, 이전 구역에서 영향을 받으면 (3-1), 안받으면 3 가지의 경우를 가진다.
2. 영향을 안 끼치는 경우의 가짓수는 항상 (전단계의 경우의 수 합) - (전단계의 갯수) 이고,
영향을 끼치는 경우의 가짓수는 (전단계의 갯수) 이다.
일부분으로 보았을때,
아래처럼 영향을 안 끼치는 경우의 가짓수는 (4 - 1) 개, 영향을 끼치는 경우는 1개로 갯수가 고정되어있는 부분을
알수 있었습니다.

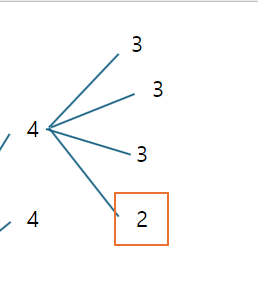
이러한 조건을 가지고, 아래와 같은 식을 구성해 주었습니다.
//temp_sum = 전단계의 합
//temp = 전 단계의 갯수
//Count = 현재 구역의 모양에 대한 경우의수 4,3,2
temp_sum = ((temp_sum - temp) * Count + temp * (Count - 1));
이제 이 식을 가지고 각 구역에 대한 경우의 수들을 구해주며, 마지막 구역까지 이동해주는 코드를 구성하면
아래처럼!
int solution(int n, vector<int> tops) {
int answer_Per = 0;
int Count = 0; // (4, 3) (3,2)
int temp = 0; // 전 단계의 갯수
int temp_sum = 0; // 전 단계의 합
int SaveTemp = 0;
for (int i = 0; i < tops.size(); i++) { // 각 삼각형에 대한 경우의 수 계산
if (temp_sum == 0) {
temp = 1;
temp_sum = tops[i] + 3;
continue;
}
if (tops[i] == 0) { // 윗 삼각형이 없는 경우
Count = 3;
}
else { // 윗삼각형이 있는경우
Count = 4;
}
cout << temp_sum << " " << temp << endl;
SaveTemp = temp_sum;
temp_sum = ((temp_sum - temp) * Count + temp * (Count - 1));
temp = SaveTemp;
temp_sum %= 10007;
temp_sum += 10007;
temp %= 10007;
}
return temp_sum % 10007;
}
끝!
여기서 +=10007연산을 해주지않아... 한참 헤맸습니다....
이 연산을 해주지 않으면 temp_sum - temp를 계산하며 음수가 나와버리는 경우가 존재합니다...
+=10007의 경우 %10007의 연산을 통해 상쇄되는 부분이기에 결과에는 영향을 끼치지 않습니다!
재귀로 풀렸다면 좋았겠지만, 식을 구하는 부분과 식의 연산 부분에 대한 오류를 고치는부분때문에
꽤 시간이 걸렸던 문제였던 것 같습니다..
그래도 끝!
ALL
#include <string>
#include <vector>
#include <iostream>
using namespace std;
int solution(int n, vector<int> tops) {
int answer_Per = 0;
int Count = 0; // (4, 3) (3,2)
int temp = 0; // 전 단계의 갯수
int temp_sum = 0; // 전 단계의 합
int SaveTemp = 0;
for (int i = 0; i < tops.size(); i++) { // 각 삼각형에 대한 경우의 수 계산
if (temp_sum == 0) {
temp = 1;
temp_sum = tops[i] + 3;
continue;
}
if (tops[i] == 0) { // 윗 삼각형이 없는 경우
Count = 3;
}
else { // 윗삼각형이 있는경우
Count = 4;
}
SaveTemp = temp_sum;
temp_sum = ((temp_sum - temp) * Count + temp * (Count - 1));
temp = SaveTemp;
temp_sum %= 10007;
temp_sum += 10007;
temp %= 10007;
}
return temp_sum % 10007;
}
틀린점이 있다면 댓 달아주세요!

'코딩테스트!(프로그래머스 & 백준) > 프로그래머스-C++' 카테고리의 다른 글
| 코딩테스트 -- 2차원 동전 뒤집기 - (프로그래머스 / C++) (0) | 2024.04.03 |
|---|---|
| 코딩테스트 -- 고고학 최고의 발견 - (프로그래머스 / C++) (0) | 2024.04.02 |
| 코딩테스트 -- [PCCP 기출문제] 4번 / 수레 움직이기 - (프로그래머스 / C++) (0) | 2024.03.19 |
| 코딩테스트 -- 상담원 인원 - (프로그래머스 / C++) (0) | 2024.03.18 |
| 코딩테스트 -- n + 1 카드게임 - (프로그래머스 / C++) (1) | 2024.03.14 |


댓글