프로그래머스
코드 중심의 개발자 채용. 스택 기반의 포지션 매칭. 프로그래머스의 개발자 맞춤형 프로필을 등록하고, 나와 기술 궁합이 잘 맞는 기업들을 매칭 받으세요.
programmers.co.kr
문제!
n개의 섬 사이에 다리를 건설하는 비용(costs)이 주어질 때, 최소의 비용으로 모든 섬이 서로 통행 가능하도록 만들 때 필요한 최소 비용을 return 하도록 solution을 완성하세요.
다리를 여러 번 건너더라도, 도달할 수만 있으면 통행 가능하다고 봅니다. 예를 들어 A 섬과 B 섬 사이에 다리가 있고, B 섬과 C 섬 사이에 다리가 있으면 A 섬과 C 섬은 서로 통행 가능합니다.
제한사항
- 섬의 개수 n은 1 이상 100 이하입니다.
- costs의 길이는 ((n-1) * n) / 2이하입니다.
- 임의의 i에 대해, costs[i][0] 와 costs[i] [1]에는 다리가 연결되는 두 섬의 번호가 들어있고, costs[i] [2]에는 이 두 섬을 연결하는 다리를 건설할 때 드는 비용입니다.
- 같은 연결은 두 번 주어지지 않습니다. 또한 순서가 바뀌더라도 같은 연결로 봅니다. 즉 0과 1 사이를 연결하는 비용이 주어졌을 때, 1과 0의 비용이 주어지지 않습니다.
- 모든 섬 사이의 다리 건설 비용이 주어지지 않습니다. 이 경우, 두 섬 사이의 건설이 불가능한 것으로 봅니다.
- 연결할 수 없는 섬은 주어지지 않습니다.
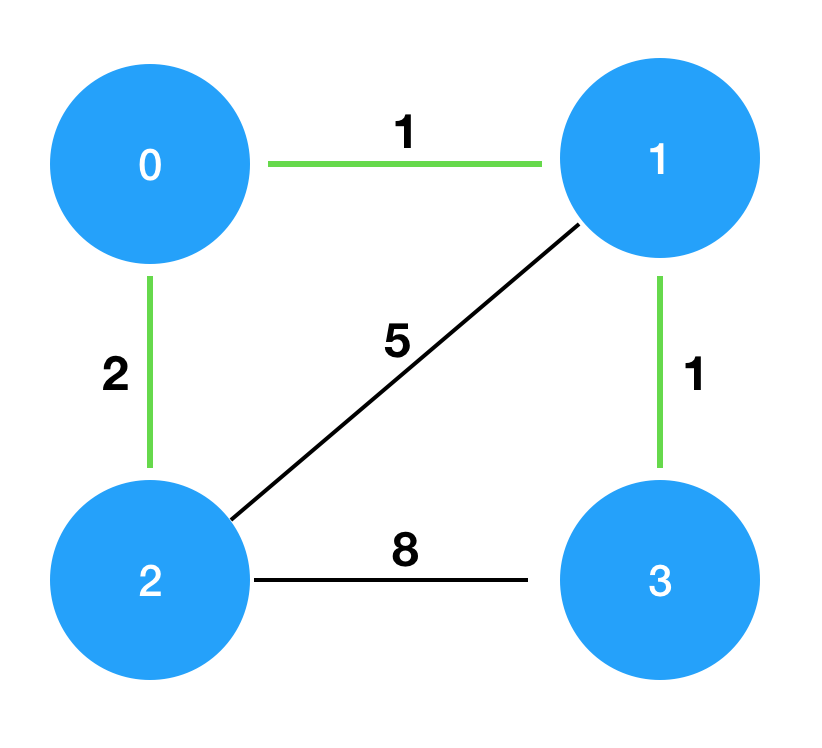
요약하면 모든섬을 연결하는 간선들을 가장 적은 비용으로 설치하는 문제....
거의 이런 문제는 그래프 탐색으로 풀었기 때문에 이번에도 그렇게 풀었습니다만....
탐색으로 풀 시에는 문제가 하나 생긴다는것을 알게되었습니다...
깊이 탐색으로 풀게되면 모든 섬이 한 경로에 모두 존재하도록 만들어집니다
하지만 아래의 경우
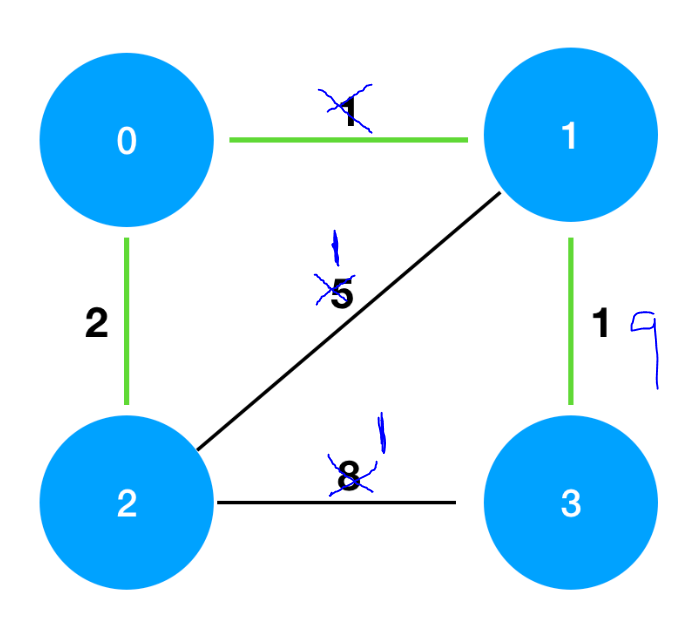
2에서 모든 섬으로 연결하는 방법이 최소이기에 2에서 3방향의 간선을 선택할것입니다...
일반적인 탐색은 한점을 탐색하고 다음 점으로 넘어가기에 위의 부분을 고려하지 못하게 됩니다..!
실패코드
아래 코드를 돌려보면 visit을 체크해주지않고 이동하기에 싸이클이 생겨 무한루프를 돌게 됩니다...!
#include <string>
#include <vector>
#include <iostream>
using namespace std;
int answer = 987654321;
int c=0;
bool check(vector<int>&visit){
for(int i:visit){
if(i==0){
return false;
}
}
return true;
}
void find(int n ,int pay,int now, vector<int>&visit, vector<vector<int>>grap){
if(check(visit)){
answer=min(answer,pay);
}
c+=1;
if(c==10){
cout<<"끝"<<endl;
return;
}
if(answer<=pay){
return;
}
for(int i=0;i<n;i++){
if(grap[now][i]!=0){
visit[i]=1;
find(n ,pay+grap[now][i],i,visit,grap);
visit[i]=0;
}
}
}
int solution(int n, vector<vector<int>> costs) {
vector<int>visit(n);
vector<vector<int>>grap(n,vector<int>(n));
for(vector<int> i : costs){
grap[i[0]][i[1]]=i[2];
grap[i[1]][i[0]]=i[2];
}
for(int i=0;i<n;i++){
visit[i]=1;
find(n,0,i,visit,grap);
visit[i]=0;
}
return answer;
}
어떻게 할까... 하다가 모든 정점을 잇는다.. = 트리!
최소 신장 트리를 만들면 되는 문제 였습니다.
최소신장트리!(프림과 크루스칼)
*그래프 내의 모든 정점을 포함하는 트리(최소로) *사이클 있으면 ㄴㄴ 프림 — 시작정점을 기준으로 신장트리를 확장— 방법은 다익스트라와 동일한거 같음! 차이점- 다익스트라는 모든정점이
ljhyunstory.tistory.com
저는 크루스칼 알고리즘을 사용했습니다! (모든 정점을 시작점으로 두고 다 확인하는 프림보다는 좋아보여서? )
크루스칼 알고리즘은 가장 작은 간선부터 사이클이 생기지않게 계속 연결하는 알고리즘으로
가장 중요한 점은 사이클이 생기지 않게! 입니다.
이 부분을 위해서 하나의 함수를 만들어 주는데, 노도들의 최산단 루트노드를 구하는 함수입니다.
int getParent(int point){
if(set[point]==point){
return point;
}
return set[point]=getParent(set[point]);
}위의 함수가 왜 필요할까?
만약 A와 C 가 있을때
A의 루트는 B, C 의 루트도 B 라고 했을때
A, C 는 같은 부모를 가지기에 연결시 싸이클이 발생합니다.
하지만 다른 부모를 가지고 있을시 연결해주어도 사이클이 생기지 않는 점을 이용하기 위해 위의 함수를 사용합니다!
이제 본격적으로 시작!
먼저 가중치가 작은 간선부터 대입할것이기에 정렬부터 해주고
bool bigyo(vector<int>a, vector<int>b){
return a[2]<b[2];
}
///~ ~ ~ ~
sort(costs.begin(),costs.end(),bigyo);//작은 순서대로
다음은 노드들의 부모를 자기 자신으로 설정 해줍시다.
int set[101];
for(int i=0;i<n;i++){
set[i]=i;
}
그리고 간선을 하나씩 추가해주며 두 노드의 부모노드를 비교! , 연결 해줍시다.
for(int i=0;i<costs.size();i++){//길이 순서대로!
int start=getParent(costs[i][0]);//각각
int end=getParent(costs[i][1]);
if(start != end){//싸이클 안생길시?
answer+=costs[i][2];
set[end]=start;//연결
}
}
여기 까지가 끝..!
크루스칼 알고리즘, 부모노드 등등 먼가 막 나와서 굉장히 복잡해질줄 알았지만
간단하게 구현되네요 ㅎ
ALL
#include <string>
#include <vector>
#include<algorithm>
#include <iostream>
using namespace std;
int set[101];
bool bigyo(vector<int>a, vector<int>b){
return a[2]<b[2];
}
int getParent(int point){
if(set[point]==point){
return point;
}
return set[point]=getParent(set[point]);
}
int solution(int n, vector<vector<int>> costs) {
// 크루스칼 알고리즘 : 가중치가 작은 간선부터 연결 -> 싸이클이 생기지 않게 계속 연결
int answer = 0;
for(int i=0;i<n;i++){
set[i]=i;
}
sort(costs.begin(),costs.end(),bigyo);//작은 순서대로
for(int i=0;i<costs.size();i++){//길이 순서대로!
int start=getParent(costs[i][0]);//각각
int end=getParent(costs[i][1]);
if(start != end){//싸이클 안생길시?
answer+=costs[i][2];
set[end]=start;//연결
}
}
return answer;
}
틀린점이 있다면 댓 달아주세요!

'코딩테스트!(프로그래머스 & 백준) > 프로그래머스-C++' 카테고리의 다른 글
| 코딩테스트 -- 외벽 점검 - (프로그래머스 / C++) (0) | 2022.07.27 |
|---|---|
| 코딩테스트 -- 단속 카메라 - (프로그래머스 / C++) (0) | 2022.07.26 |
| 코딩테스트 -- 모두 0으로 만들기 - (프로그래머스 / C++) (0) | 2022.07.23 |
| 코딩테스트 -- 징검다리 건너기 - (프로그래머스 / C++) (0) | 2022.07.22 |
| 코딩테스트 -- 길 찾기 게임 - (프로그래머스 / C++) (0) | 2022.07.21 |




댓글